Neural Networks: How Machines Learn to Think

Introduction
In recent years, neural networks have moved from the pages of research papers into the heart of everyday life. They drive the recommendations we see on streaming platforms, power the large language models that do your banco and even help create life like images. Inspired loosely by the way the human brain processes information, neural networks are designed to recognise patterns, learn from data, and make predictions across many domains. This article will explain how neural networks are structured, how they learn.
Iterative process when training (high level overview)
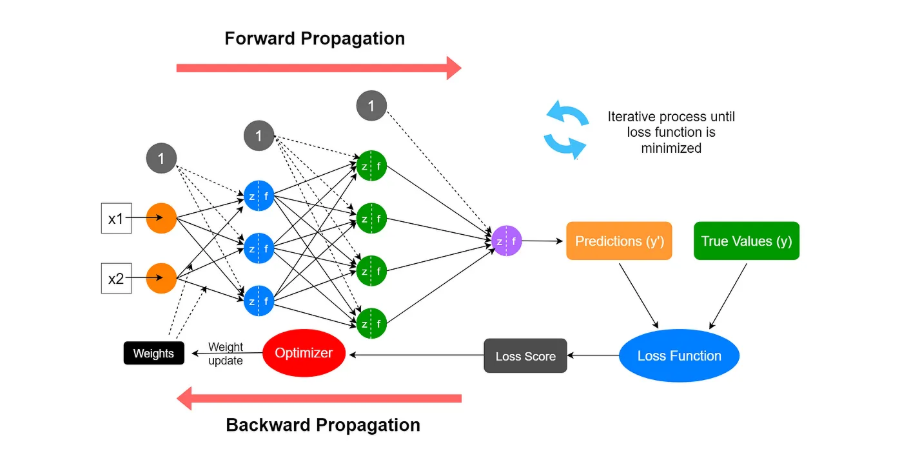
Forward propagation
Think of the neural network as a function with x1, x2 as the input. Each node’s output is calculated by: activation_function(w*a+w*a…+b).
Training data gets fed through the network and generates an output y’. It is easier to understand if you focus on a single node instead of the whole network. The ‘non-linearity’ in the diagram is the activation function. The summation symbol is used instead of adding all w*a together. Y_hat is the output of that single node. This process occurs layer by layer until you reach the output layer.
Loss calculation
This is when the prediction is compared to the true value by plugging it in a loss function with inputs y’ (your prediction) and y (true value). All training data has a true value. You may ask ‘why can’t you just use the number of incorrect predictions as the loss?’. The purpose of the loss function is to create a smooth continuous function to update parameters. For instance, if the network goes from predicting 0.45 to 0.49 when the correct answer is 1, it is getting better but number of incorrect predictions would still be the same.
A classic loss function is the Mean Squared Error. You take the average over all the
training data for the calculation (answer-your_prediction)^2
Back propagation
The loss calculation’s output is used to tweak the parameters in the neural network to minimise the loss. This is the most technical part of neural networks. The basic idea is that there is a way to find how to change the parameters to minimise the loss by finding out the gradient (dc/dw or dc/db).
Using the chain rule of calculus, the algorithm calculates how much each weight and bias contributed to the error, then updates them slightly (via gradient descent) to reduce future mistakes. Gradient Descent works by adjusting the parameters (weights and biases) by subtracting the gradients dc/dw and dc/db. This gradient tells us the slope (which way is uphill). The subtraction makes it step downhill toward the minimum. There is also a learning rate (a) which controls how big each step is so we don’t overshoot the minimum.
In a nutshell
Imagine you are a student preparing for weekly tests. At first, your study habits are random: maybe you stay up late, skip revision, or drink too much caffeine. After each test, you get a score. That score acts like feedback: the lower it is, the higher your “loss”. You then reflect on what habits you had before the test and adjust them accordingly. You might choose to sleep earlier, to study more consistently, or to eat healthier. Over many weeks, this cycle of test > feedback > adjustment gradually improves your performance. Just like a neural network, you learn which “parameters” (i.e. habits) lead to better results, until eventually you are scoring close to 100% every time.
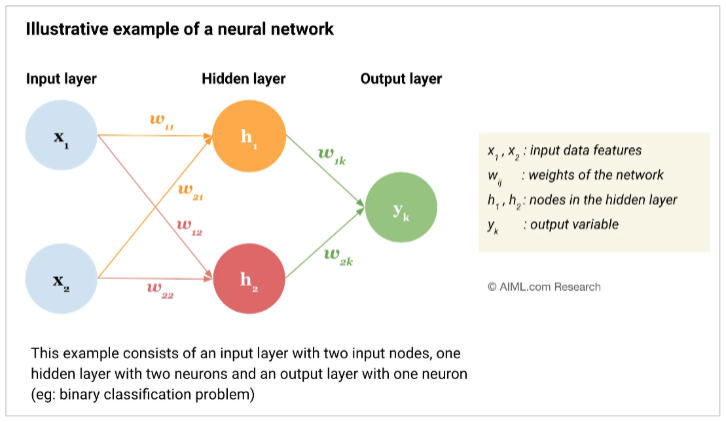
A brief overview of parameters in a neural network is as follows:
Layers: layers include the input layer where the
input is fed in, the hidden layer which processes the data and the output layer where the prediction is given. Layers can have n number of nodes (two in this diagram for input and hidden). You can also add more hidden layers for more sophisticated predictions.
Weights: each edge has a weight as shown in the diagram. The weights are used to scale the inputs.
Biases: each node other than the ones in the input layer has a bias associated with it. This allows for more complex behaviour with the neurons when combined with the activation function. E.g. h1, h2, yk all have unique biases
The activation function: this is a non linear function. Without it, the entire neural network would just be a really long linear model. It helps capture complex patterns in the data.
Conclusion
Neural networks are computational systems that mimic the brain’s way of learning from data. They use layers of interconnected nodes, weighted connections, and activation functions to recognise patterns and make decisions. Over time, they adjust based on feedback, improving their accuracy and performance. As neural networks become more interwoven with everyday life, it is important to understand how they work. By gaining this understanding, we can harness their potential responsibly and make informed choices about their use.